how many total hydrogen atoms are in this solution
Atomic Structure
57 The Hydrogen Corpuscle
Acquisition Objectives
By the end of this section, you will follow healthy to:
- Describe the hydrogen atom in price of wave function, probability density, tally muscularity, and orbital angular momentum
- Identify the corporal import of each of the quantum numbers (
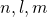 ) of the atomic number 1 particle
) of the atomic number 1 particle - Signalize between the Bohr and Schrödinger models of the atom
- Function quantum numbers to calculate of the essence information about the hydrogen atom
The H atom is the simplest atom in nature and, therefore, a good opening point to canvas atoms and substance structure. The hydrogen corpuscle consists of a unary negatively charged electron that moves about a positively charged proton ((Figure)). In Niels Henrik David Bohr's model, the electron is pulled around the proton in a perfectly circular field past an mesmeric Coulomb pull back. The proton is approximately 1800 multiplication more massive than the electron, so the proton moves very little in response to the force on the proton by the electron. (This is analogous to the Earth-Sun system, where the Sunshine moves very little in response to the coerce exerted on it by Earth.) An explanation of this effect victimization Newton's laws is presumption in Photons and Matter Waves.
A representation of the Niels Henrik David Bohr model of the hydrogen atom.
With the assumption of a determinate proton, we direction on the move of the electron.
In the electric car field of the proton, the potential energy of the electron is
![]()
where ![]() and r is the distance between the electron and the proton. As we saw earlier, the force out on an object is equal to the negative of the gradient (or slope) of the potential energy function. For the special case of a atomic number 1 atom, the pull out betwixt the negatron and proton is an attractive Coulomb force.
and r is the distance between the electron and the proton. As we saw earlier, the force out on an object is equal to the negative of the gradient (or slope) of the potential energy function. For the special case of a atomic number 1 atom, the pull out betwixt the negatron and proton is an attractive Coulomb force.
Notice that the potential vigor officiate U(r) does not vary in sentence. As a result, Schrödinger's equation of the hydrogen atom reduces to two simpler equations: one that depends only if on space (x, y, z) and another that depends only on time (t). (The separation of a wave function into space- and prison term-unfree parts for time-self-sufficient potential energy functions is discussed in Quantum Mechanics.) We are most interested in the space-dependent equation:
![]()
where ![]() is the boxy wave use of the electron,
is the boxy wave use of the electron, ![]() is the mass of the negatron, and E is the total energy of the electron. Recall that the total wave function
is the mass of the negatron, and E is the total energy of the electron. Recall that the total wave function ![]() is the product of the space-dependent wave function
is the product of the space-dependent wave function ![]() and the time-dependent wave function
and the time-dependent wave function ![]() .
.
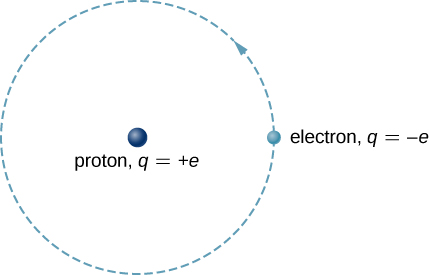
In addition to being time-independent, U(r) is also spherically centrosymmetric. This suggests that we may solve Schrödinger's equation to a greater extent easily if we express it in terms of the round shape coordinates ![]() instead of orthogonal coordinates
instead of orthogonal coordinates ![]() . A spherical coordinate system is shown in (Figure). In spherical coordinates, the variable r is the radial coordinate,
. A spherical coordinate system is shown in (Figure). In spherical coordinates, the variable r is the radial coordinate, ![]() is the polar tip over (relative to the vertical z-axis), and
is the polar tip over (relative to the vertical z-axis), and ![]() is the azimuthal angle (relative to the x-axis). The family relationship between spherical and angulate coordinates is
is the azimuthal angle (relative to the x-axis). The family relationship between spherical and angulate coordinates is ![]()
The relationship 'tween the spherical and rectangular equal systems.
The factor ![]() is the order of magnitude of a vector formed by the projection of the pivotal vector onto the XY-plane. Also, the coordinates of x and y are obtained aside projecting this transmitter onto the x– and y-axes, severally. The inverse transformation gives
is the order of magnitude of a vector formed by the projection of the pivotal vector onto the XY-plane. Also, the coordinates of x and y are obtained aside projecting this transmitter onto the x– and y-axes, severally. The inverse transformation gives
![]()
Schrödinger's roll equation for the hydrogen particle in spherical coordinates is discussed in more progressive courses in modern physics, so we do not consider it in detail here. Still, due to the spherical isotropy of U(r), this equality reduces to three simpler equations: one for all of the ternary coordinates ![]() Solutions to the clock-independent beckon serve are written arsenic a production of three functions:
Solutions to the clock-independent beckon serve are written arsenic a production of three functions:
![]()
where R is the radial-ply tire affair dependent on the radial coordinate r only; ![]() is the polar function bloodsucking on the polar coordinate
is the polar function bloodsucking on the polar coordinate ![]() only; and
only; and ![]() is the phi go of
is the phi go of ![]() exclusive. Valid solutions to Schrödinger's equation
exclusive. Valid solutions to Schrödinger's equation ![]() are labeled aside the quantum numbers n, l, and m.
are labeled aside the quantum numbers n, l, and m.

(The reasons for these names will glucinium explained in the incoming section.) The radial function R depends only on n and l; the polar subroutine ![]() depends only on l and m; and the phi function
depends only on l and m; and the phi function ![]() depends only on m. The dependence of each function along quantum numbers is indicated with subscripts:
depends only on m. The dependence of each function along quantum numbers is indicated with subscripts:
![]()
Not all sets of quantum numbers racket (n, l, m) are executable. For example, the orbital angular quantum number l keister never be greater or equal to the star quantum number ![]() . Specifically, we have
. Specifically, we have
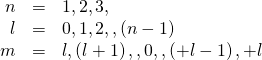
Notice that for the priming state, ![]() ,
, ![]() , and
, and ![]() . Put differently, on that point is exclusively one quantum state with the wave function for
. Put differently, on that point is exclusively one quantum state with the wave function for ![]() , and information technology is
, and information technology is ![]() . Yet, for
. Yet, for ![]() , we give
, we give
![]()
Therefore, the allowed states for the ![]() state are
state are ![]() ,
, ![]() , and
, and ![]() . Model undulate functions for the hydrogen atom are inclined in (Figure). Note that some of these expressions contain the letter i, which represents
. Model undulate functions for the hydrogen atom are inclined in (Figure). Note that some of these expressions contain the letter i, which represents ![]() . When probabilities are calculated, these Byzantine numbers do non look in the final answer.
. When probabilities are calculated, these Byzantine numbers do non look in the final answer.
| | |
| | |
| | |
| | |
| | |
Corporeal Import of the Quantum Numbers
Each of the three quantum numbers of the hydrogen atom (n, l, m) is associated with a contrary physical quantity. The principal quantum number n is associated with the total energy of the electron, ![]() . According to Schrödinger's equation:
. According to Schrödinger's equation:
![]()
where ![]() Notice that this expression is identical to that of Bohr's model. As in the Niels Bohr model, the negatron in a item state of energy does non shine.
Notice that this expression is identical to that of Bohr's model. As in the Niels Bohr model, the negatron in a item state of energy does non shine.
How Many Possible States? For the hydrogen particle, how many possible quantum states correspond to the principal number ![]() ? What are the energies of these states?
? What are the energies of these states?
Scheme For a hydrogen atom of a given energy, the numeral of allowed states depends on its orbital angular momentum. We can count these states for each value of the principal quantum number, ![]() However, the total vitality depends on the principal quantum telephone number only, which substance that we can use (Figure) and the number of states counted.
However, the total vitality depends on the principal quantum telephone number only, which substance that we can use (Figure) and the number of states counted.
Solution If ![]() , the allowed values of l are 0, 1, and 2. If
, the allowed values of l are 0, 1, and 2. If ![]() ,
, ![]() (1 state). If
(1 state). If ![]() ,
, ![]() (3 states); and if
(3 states); and if ![]() ,
, ![]() (5 states). In total, there are
(5 states). In total, there are ![]() allowed states. Because the total energy depends only on the principal quantum number,
allowed states. Because the total energy depends only on the principal quantum number, ![]() , the energy of each of these states is
, the energy of each of these states is
![]()
Significance An negatron in a atomic number 1 atom can occupy galore different angular momentum states with the really same energy. As the orbital angular momentum increases, the number of the allowed states with the assonant energy increases.
The angular momentum orbital quantum list l is associated with the itinerary tricuspid impulse of the electron in a hydrogen spec. Quantum theory tells us that when the hydrogen molecule is in the state ![]() , the magnitude of its orbital angular momentum is
, the magnitude of its orbital angular momentum is
![]()
where
![]()
This result is somewhat antithetical from that ground with Niels Henrik David Bohr's theory, which quantizes angular momentum according to the rule ![]()
Quantum states with different values of cavity angular momentum are distinguished using qualitative analysis annotation ((Pattern)). The designations s, p, d, and f result from early historical attempts to classify thermonuclear spectral lines. (The letters brook for sharp, principal, interpenetrate, and fundamental, severally.) After f, the letters carry on alphabetically.
The ground state of atomic number 1 is designated as the 1s state, where "1" indicates the energy level ![]() and "s" indicates the orbital angular impulse state (
and "s" indicates the orbital angular impulse state (![]() ). When
). When ![]() , l can glucinium either 0 or 1. The
, l can glucinium either 0 or 1. The ![]() ,
, ![]() state is designated "2s." The
state is designated "2s." The ![]() ,
, ![]() state is designated "2p." When
state is designated "2p." When ![]() , l can be 0, 1, or 2, and the states are 3s, 3p, and 3d, respectively. Notation for other quantum states is given in (Figure).
, l can be 0, 1, or 2, and the states are 3s, 3p, and 3d, respectively. Notation for other quantum states is given in (Figure).
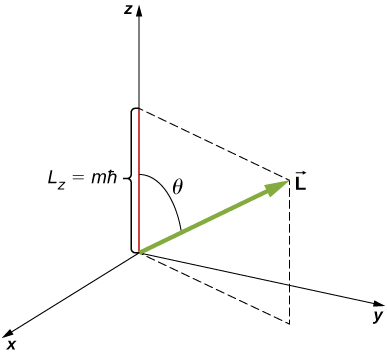
The bicuspid momentum projection quantum number m is associated with the azimuthal angle ![]() (see (Figure)) and is related to the z-part of orbital angular momentum of an electron in a atomic number 1 atom. This component is given by
(see (Figure)) and is related to the z-part of orbital angular momentum of an electron in a atomic number 1 atom. This component is given by
![]()
where
![]()
The z-component of square-shaped momentum is connected the magnitude of angular momentum away
![]()
where ![]() is the angle betwixt the angular momentum vector and the z-axis. Mention that the direction of the z-axis is determined by experiment—that is, along any direction, the experimenter decides to measure the cuspidate impulse. For example, the z-direction might gibe to the direction of an extraneous magnetic athletic field. The family relationship 'tween
is the angle betwixt the angular momentum vector and the z-axis. Mention that the direction of the z-axis is determined by experiment—that is, along any direction, the experimenter decides to measure the cuspidate impulse. For example, the z-direction might gibe to the direction of an extraneous magnetic athletic field. The family relationship 'tween ![]() is given in (Figure out).
is given in (Figure out).
The z-component part of space momentum is quantized with its own quantum number m.
| Orbital Quantum Total l | Angular Impulse | Body politic | Spectroscopic Name |
|---|---|---|---|
| 0 | 0 | s | Sharp |
| 1 | | p | Principal |
| 2 | | d | Diffuse |
| 3 | | f | Fundamental |
| 4 | | g | |
| 5 | | h |
| | | | | | | |
| | 1s | |||||
| | 2s | 2p | ||||
| | 3s | 3p | 3d | |||
| | 4s | 4p | 4d | 4f | ||
| | 5s | 5p | 5d | 5f | 5g | |
| | 6s | 6p | 6d | 6f | 6g | 6h |
The quantisation of ![]() is equivalent to the quantization of
is equivalent to the quantization of ![]() . Subbing
. Subbing ![]() for L and m for
for L and m for ![]() into this equation, we ascertain
into this equation, we ascertain
![]()
Thus, the angle ![]() is amount with the particular values
is amount with the particular values
![]()
Notice that both the south-polar angle (![]() ) and the project of the angular momentum vector onto an arbitrary z-axis (
) and the project of the angular momentum vector onto an arbitrary z-axis (![]() ) are quantized.
) are quantized.
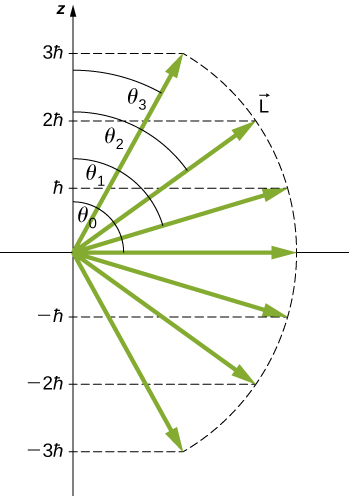
The quantization of the polar angle for the ![]() state is shown in (Figure). The orbital angular momentum vector lies somewhere on the surface of a cone cell with an opening angle
state is shown in (Figure). The orbital angular momentum vector lies somewhere on the surface of a cone cell with an opening angle ![]() relative to the z-Axis (unless
relative to the z-Axis (unless ![]() in which case
in which case ![]() and the vector points are perpendicular to the z-axis).
and the vector points are perpendicular to the z-axis).
The quantization of orbital angular momentum. Each vector lies on the surface of a cone with axis along the z-axis.
A elaborated study of cuspate impulse reveals that we cannot bon entirely three components at the same time. In the previous section, the z-component of route angular momentum has definite values that depend on the quantum number m. This implies that we cannot know both x- and y-components of triangular momentum, ![]() and
and ![]() , with certainty. As a result, the accurate management of the orbital angular momentum vector is unknown.
, with certainty. As a result, the accurate management of the orbital angular momentum vector is unknown.
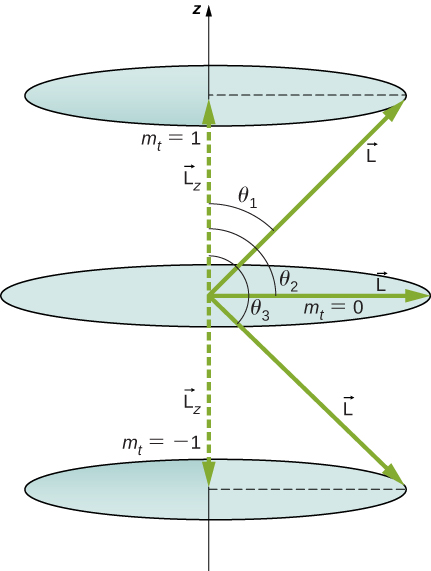
What Are the Allowed Directions? Calculate the angles that the angular momentum vector ![]() can do with the z-axis for
can do with the z-axis for ![]() , every bit shown in (Figure).
, every bit shown in (Figure).
The component of a given angulate impulse along the z-axis vertebra (settled away the direction of a attractive force field) can have only certain values. These are shown here for ![]() , for which
, for which ![]() The direction of
The direction of ![]() is quantized in the sentience that it arse make only certain angles relative to the z-axis.
is quantized in the sentience that it arse make only certain angles relative to the z-axis.
Scheme The vectors ![]() and
and ![]() (in the z-steering) form a right triangle, where
(in the z-steering) form a right triangle, where ![]() is the hypotenuse and
is the hypotenuse and ![]() is the adjacent side. The ratio of
is the adjacent side. The ratio of ![]() to |
to |![]() | is the cos of the angle of interest. The magnitudes
| is the cos of the angle of interest. The magnitudes ![]() and
and ![]() are given by
are given by
![]()
Solution We are given ![]() , so ml can comprise
, so ml can comprise ![]() Thusly, L has the value given by
Thusly, L has the value given by
![]()
The quantity ![]() can take three values, given by
can take three values, given by ![]() .
.
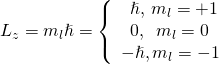
As you can see in (Figure), ![]() sol for
sol for ![]() , we have
, we have
![]()
Thus,
![]()
Similarly, for ![]() , we find
, we find ![]() this gives
this gives
![]()
Then for ![]() :
:
![]()
so that
![]()
Significance The angles are reproducible with the figure. Exclusively the angle proportionate to the z-axis is quantized. L can detail in any direction as long as IT makes the proper lean on with the z-Axis. Frankincense, the angular impulse vectors lie on cones, as illustrated. To see how the correspondence principle holds here, consider that the smallest angle (![]() in the exercise) is for the maximum value of
in the exercise) is for the maximum value of ![]() namely
namely ![]() For that smallest angle,
For that smallest angle,
![]()
which approaches 1 as l becomes very large. If ![]() , so
, so ![]() . Moreover, for large l, there are many an values of
. Moreover, for large l, there are many an values of ![]() , thus that all angles become possible as l gets very large.
, thus that all angles become possible as l gets very large.
Check Your Discernment Can the order of magnitude of ![]() ever be adequate L?
ever be adequate L?
No. The quantum number ![]() Thus, the magnitude of
Thus, the magnitude of ![]() is always little than L because
is always little than L because ![]()
Using the Wave Function to Give Predictions
As we saw earlier, we can use quantum mechanics to make predictions about physical events by the use of chance statements. It is therefore proper to state, "An electron is located within this volume with this probability at this time," but non, "An negatron is located at the position (x, y, z) at this clock time." To determine the probability of finding an electron in a hydrogen particle in a particular region of space, IT is necessary to integrate the probability density ![]() over that part:
over that part:
![]()
where dV is an infinitesimal volume ingredient. If this intrinsical is computed for all space, the result is 1, because the probability of the particle to be placed somewhere is 100% (the normalization condition). In a Thomas More sophisticated course on fashionable physics, you will find that ![]() where
where ![]() is the complex conjugate. This eliminates the occurrences of
is the complex conjugate. This eliminates the occurrences of ![]() in the above figuring.
in the above figuring.
Deliberate an electron in a state of zero angular momentum (![]() ). In this case, the electron's wave operate depends only on the radial ordinate r. (Relate to the states
). In this case, the electron's wave operate depends only on the radial ordinate r. (Relate to the states ![]() and
and ![]() in (Figure).) The infinitesimal volume element corresponds to a spherical shell of wheel spoke r and infinitesimal thickness dr, graphic As
in (Figure).) The infinitesimal volume element corresponds to a spherical shell of wheel spoke r and infinitesimal thickness dr, graphic As
![]()
The probability of finding the negatron in the region r to ![]() ("at about r") is
("at about r") is
![]()
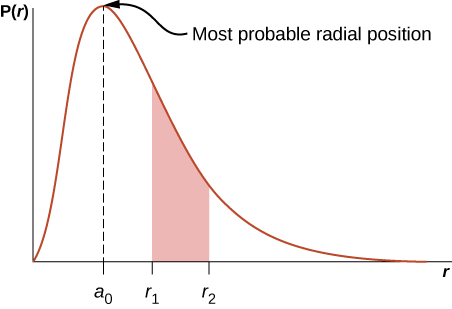
Here P(r) is named the radial probability density function (a probability per unit length). For an negatron in the ground state of atomic number 1, the probability of finding an electron in the region r to ![]() is
is
![]()
where ![]() angstroms. The radial probability concentration function P(r) is plotted in (Figure). The area under the curve between any two radial positions, say
angstroms. The radial probability concentration function P(r) is plotted in (Figure). The area under the curve between any two radial positions, say ![]() and
and ![]() , gives the probability of finding the negatron in this radial range. To find the most probable radial position, we set the firstborn derivative of this go to zero (
, gives the probability of finding the negatron in this radial range. To find the most probable radial position, we set the firstborn derivative of this go to zero (![]() ) and solve for r. The most equiprobable radial position is not equivalent to the average operating theater expectation value of the stellate posture because
) and solve for r. The most equiprobable radial position is not equivalent to the average operating theater expectation value of the stellate posture because ![]() is not symmetrical about its peak value.
is not symmetrical about its peak value.
The visible radiation chance density function for the ground state of hydrogen.
If the electron has path space impulse (![]() ), and then the waving functions representing the electron depend on the angles
), and then the waving functions representing the electron depend on the angles ![]() and
and ![]() that is,
that is, ![]()
![]() (r,
(r, ![]() ,
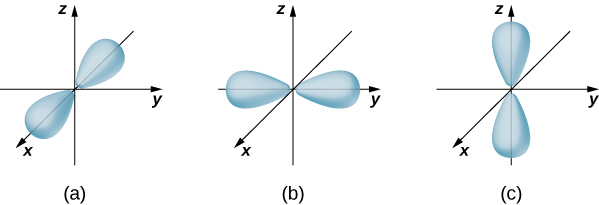
, ![]() ). Microscopical orbitals for deuce-ac states with
). Microscopical orbitals for deuce-ac states with ![]() and
and ![]() are shown in (Figure). An atomic orbital is a region in space that encloses a certain percentage (ordinarily 90%) of the electron probability. (Sometimes atomic orbitals are referred to as "clouds" of probability.) Notice that these distributions are pronounced in sure directions. This directionality is important to chemists when they analyse how atoms are bound unneurotic to form molecules.
are shown in (Figure). An atomic orbital is a region in space that encloses a certain percentage (ordinarily 90%) of the electron probability. (Sometimes atomic orbitals are referred to as "clouds" of probability.) Notice that these distributions are pronounced in sure directions. This directionality is important to chemists when they analyse how atoms are bound unneurotic to form molecules.
The probability density distributions for three states with ![]() and
and ![]() . The distributions are directed along the (a) x-Axis, (b) y-bloc, and (c) z-axis.
. The distributions are directed along the (a) x-Axis, (b) y-bloc, and (c) z-axis.
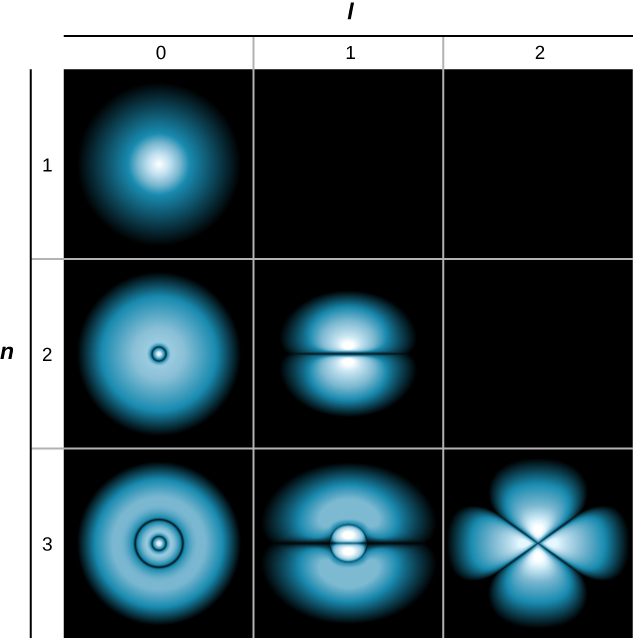
A slightly different representation of the wave function is given in (Figure). In this case, light and dark regions point locations of relatively high and low probability, respectively. In contrast to the Niels Bohr model of the hydrogen atom, the electron does not turn the proton nucleus in a well-defined path. Indeed, the uncertainty rule makes it impossible to know how the negatron gets from unity place to another.
Probability clouds for the electron in the ground state and several worked up states of hydrogen. The chance of determination the negatron is indicated past the shade of color; the lighter the color, the greater the gamble of determination the electron.
Unofficial
- A hydrogen atom commode represent described in terms of its wave function, probability density, sum up vigour, and orbital angular momentum.
- The state of an electron in a hydrogen mote is specified by its quantum Numbers (n, l, m).
- In contrast to the Bohr model of the atom, the Schrödinger framework makes predictions based on probability statements.
- The quantum numbers of a hydrogen atom can be wont to calculate important info about the atom.
Conceptual Questions
Identify the physical implication of each of the quantum numbers of the hydrogen atom.
n (principal quantum number) ![]() total energy
total energy
![]() (cavity bicuspidate quantum number)
(cavity bicuspidate quantum number) ![]() total absolute magnitude of the orbital angular impulse
total absolute magnitude of the orbital angular impulse
m (orbital angular projection quantum number) ![]() z-component of the orbital square impulse
z-component of the orbital square impulse
Describe the ground state of hydrogen in terms of curl function, chance tightness, and atomic orbitals.
Distinguish between Bohr's and Schrödinger's mock up of the hydrogen atom. Particularly, equate the energy and route angular momentum of the ground states.
The Bohr model describes the electron as a corpuscle that moves around the proton in well-delimited orbits. Schrödinger's model describes the electron As a wave, and knowledge about the position of the negatron is restricted to probability statements. The tot up vim of the electron in the ground country (and entirely excited states) is the same for both models. However, the itinerary angular momentum of the ground state is different for these models. In Bohr's model, ![]() , and in Schrödinger's model,
, and in Schrödinger's model, ![]() .
.
Problems
The wave social occasion is evaluated at rectangular coordinates (![]() )
) ![]() (2, 1, 1) in arbitrary units. What are the spherical coordinates of this position?
(2, 1, 1) in arbitrary units. What are the spherical coordinates of this position?
![]()
If an atom has an negatron in the ![]() State Department with
State Department with ![]() , what are the executable values of l?
, what are the executable values of l?
What are the possible values of m for an electron in the ![]() state?
state?
![]() are possible
are possible
What, if some, constraints does a appreciate of ![]() direct on the other quantum numbers for an electron in an atom?
direct on the other quantum numbers for an electron in an atom?
What are the possible values of m for an electron in the ![]() state?
state?
![]() are possible
are possible
(a) How many angles can L make with the z-axis for an ![]() electron? (b) Calculate the prise of the smallest angle.
electron? (b) Calculate the prise of the smallest angle.
The force connected an electron is "negative the slope of the potential energy function." Use this knowledge and (Figure) to show that the military group on the electron in a hydrogen atom is surrendered by Coulomb's force constabulary.
![]()
What is the total number of states with cavity triangular impulse ![]() ? (Neglect electron tailspin.)
? (Neglect electron tailspin.)
The undulation function is evaluated at spherical coordinates ![]() where the time value of the radial coordinate is inclined in arbitrary units. What are the rectangular coordinates of this position?
where the time value of the radial coordinate is inclined in arbitrary units. What are the rectangular coordinates of this position?
(1, 1, 1)
Coulomb's force law states that the ram down between two charged particles is:
![]() Use this expression to determine the potential energy subprogram.
Use this expression to determine the potential energy subprogram.
Study hydrogen in the earth country, ![]() . (a) Use the derivative to determine the radial berth for which the probability tightness, P(r), is a maximum.
. (a) Use the derivative to determine the radial berth for which the probability tightness, P(r), is a maximum.
(b) Use the integral concept to determine the norm radial position. (This is called the expectation value of the electron's radial position.) Express your answers into damage of the Bohr radius, ![]() . Tip: The expectation value is the honourable average esteem. (c) Why are these values different?
. Tip: The expectation value is the honourable average esteem. (c) Why are these values different?
What is the probability that the 1s negatron of a hydrogen atom is base outside the Niels Bohr radius?
The chance that the 1s electron of a hydrogen atom is found extraneous of the Niels Bohr r is ![]()
How many polar angles are possible for an electron in the ![]() state?
state?
What is the level bes number of orbital angular impulse electron states in the ![]() shell of a hydrogen corpuscle? (Ignore negatron tailspin.)
shell of a hydrogen corpuscle? (Ignore negatron tailspin.)
For ![]() ,
, ![]() (1 state), and
(1 state), and ![]() (3 states). The total is 4.
(3 states). The total is 4.
What is the supreme act of orbital angular momentum electron states in the ![]() shell of a hydrogen atom? (Ignore electron twist.)
shell of a hydrogen atom? (Ignore electron twist.)
Glossary
- bicuspid momentum orbital quantum bi (l)
- quantum number associated with the orbital angular momentum of an electron in a hydrogen atom
- angular momentum projection quantum number (m)
- quantum total joint with the z-component of the orbital angular momentum of an electron in a hydrogen atom
- atomic orbital
- region in space that encloses a certain percentage (usually 90%) of the electron chance
- corpus quantum number (n)
- quantum number associated with the total get-up-and-go of an electron in a hydrogen atom
- radial probability density function
- function use to determine the chance of a electron to embody found in a spatial interval in r
how many total hydrogen atoms are in this solution
Source: https://opentextbc.ca/universityphysicsv3openstax/chapter/the-hydrogen-atom/
Posting Komentar untuk "how many total hydrogen atoms are in this solution"